Alloy*: A Higher-Order Relational Constraint Solver
about alloy*
- retains the syntax of Alloy: predicate logic + relational algebra
- permits higher-order quantification: changes the semantics of Alloy only by expanding the set of specifications that can be analyzed
- implements CEGIS on top of Kodkod: all higher-order quantifiers are analyzable (regardless of their position in the formula)
- applications: synthesis, game theory, minimization/maximization, ...
- papers: ICSE 2015, FMSD 2017
sample models
- sygus
- syntax guided program synthesis benchmarks
- margrave
- Margrave policy synthesizer
- graph
- various graph algorithms
select menu: File -> Open Sample Models choose path: "models/hol"
examples
Turan's graph theorem
The formulation of Turan's theorem states that a
k+1-free graph with n nodes can maximally
have (k-1)n2/(2k) edges. A graph
is k+1-free if it contains no clique
with k+1 nodes (a clique is a subset of nodes in which
every two nodes are connected by an edge); this is equivalent to
saying that its maximum clique has exactly k nodes. A
formalization of Turan's theorem in Alloy is given in the figure on
the right.
The formalization of the maxClique property is
higher-order, because it quantifies over all possible
sets of Nodes to assert that there does not exist another
set of nodes which is a clique and has more nodes than
the max-clique. Higher-order specifications are expressible in Alloy,
but the official Alloy Analyzer is not powerful enough to analyze
them. In Alloy*, in contrast, this check can be
automatically performed to confirm that no counterexample can be found
within the specified scope.
There are two ways to now formalize Turan's theorem
(the Turan_dom_constr and Turan_classical
commands). In both cases, the idea is to asserts that for all
possible edge relations (from Node
to Node) that are symmetric and irreflexive, if the
max-clique in that graph has k nodes
(k=#mClq), the number of selected edges
(e=(#edges).div[2]) must be at
most (k-1)n2/(2k) (the number of tuples in
edges is divided by 2 because the graph in
setup of the theorem in undirected). The differences, although
syntactic, have significant impact on performance:
- classical
- the classical way to constrain the domain of a universal quantifier (e.g., all edges that are symmetric and irreflexive) is to use an implication in the quantifier body; similarly, to constraint the domain of an existential quantifier (e.g., some set of nodes that is max-clique), a conjunction in the body is used.
- with domain
constraints - for an efficient CEGIS
implementation, we prefer domain constraints to be given explicitly
(as opposed to merged and inlined in the quantifier body) using the
newly introduced
whenclause (not available in standard Alloy).
| command\scope | 5 | 6 | 7 | 8 | 9 | 10 |
Turan_classical |
4s | 10s | 43s | to | to | to |
Turan_dom_constr |
0.3s | 3s | 6s | 10s | 44s | 170s |
| comparison of analysis times for various scopes | ||||||
some sig Node {} // between every two nodes there is an edge pred clique[edges: Node -> Node, clq: set Node] { all disj n1, n2: clq | n1 -> n2 in edges } // no other clique with more nodes pred maxClique[edges: Node -> Node, clq: set Node] { clique[edges, clq] no cq2: set Node | cq2!=clq && clique[edges,cq2] && #cq2>#clq } // symmetric and irreflexive pred edgeProps[edges: Node -> Node] { (~edges in edges) and (no edges & iden) } // max number of edges in a (k+1)-free graph with n // nodes is (k-1)n^2/(2k) check Turan_dom_constr { all edges: Node -> Node when edgeProps[edges] | some mClq: set Node when maxClique[edges, mClq] | let n = #Node, k = #mClq, e = (#edges).div[2] | e <= k.minus[1].mul[n].mul[n].div[2].div[k] }for 7 but 0..294 Int -- checks in ~6s // same as above, but with inlined domain constraints check Turan_classical { all edges: Node -> Node | edgeProps[edges] implies { some mClq: set Node { maxClique[edges, mClq] let n = #Node, k = #mClq, e = (#edges).div[2] | e <= k.minus[1].mul[n].mul[n].div[2].div[k] } } } for 7 but 0..294 Int -- checks in ~43s
program synthesis
program ast
abstract sig Bool {} one sig BoolTrue extends Bool {} one sig BoolFalse extends Bool {} abstract sig Node {} abstract sig BoolNode extends Node {} abstract sig IntNode extends Node {} abstract sig Var extends IntNode {} abstract sig IntLit extends IntNode { val: one Int } abstract sig IntComp extends BoolNode { left, right: IntNode } abstract sig BoolComp extends BoolNode { left, right: BoolNode } sig EQ, GTE, LTE, GT, LT extends IntComp {} sig And, Or extends BoolComp {} sig Not extends BoolNode { arg: BoolNode } sig ITE extends IntNode { condition: BoolNode, then, elsen: IntNode }
invariants
pred acyclic[r: univ->univ, s: set univ] { all x: s | x !in x.^r } fact { acyclic[arg + condition + then + elsen + IntComp<:left + IntComp<:right + BoolComp<:left + BoolComp<:right, Node] }
semantics
pred semantics[eval: Node -> (Int + Bool)] { all n: ITE { eval[n] in Int eval[n.condition] in Bool && eval[n.then] in Int && eval[n.elsen] in Int eval[n.condition] = BoolTrue implies eval[n.then] = eval[n] else eval[n.elsen] = eval[n] } all n: BoolNode | eval[n] in Bool all n: IntComp | eval[n.left] in Int and eval[n.right] in Int all n: BoolComp | eval[n.left] in Bool and eval[n.right] in Bool all v: Var | one eval[v] and eval[v] in Int all i: IntLit | one eval[i] and eval[i] in Int and eval[i] = i.val all n: Not | eval[n.arg] in Bool all n: EQ | eval[n.left] = eval[n.right] implies eval[n] = BoolTrue else eval[n] = BoolFalse all n: GTE | eval[n.left] >= eval[n.right] implies eval[n] = BoolTrue else eval[n] = BoolFalse all n: LTE | eval[n.left] <= eval[n.right] implies eval[n] = BoolTrue else eval[n] = BoolFalse all n: GT | eval[n.left] > eval[n.right] implies eval[n] = BoolTrue else eval[n] = BoolFalse all n: LT | eval[n.left] < eval[n.right] implies eval[n] = BoolTrue else eval[n] = BoolFalse all n: And | (eval[n.left] = BoolTrue and eval[n.right] = BoolTrue) implies eval[n] = BoolTrue else eval[n] = BoolFalse all n: Or | (eval[n.left] = BoolTrue or eval[n.right] = BoolTrue) implies eval[n] = BoolTrue else eval[n] = BoolFalse all n: Not | eval[n.arg] = BoolFalse implies eval[n] = BoolTrue else eval[n] = BoolFalse }
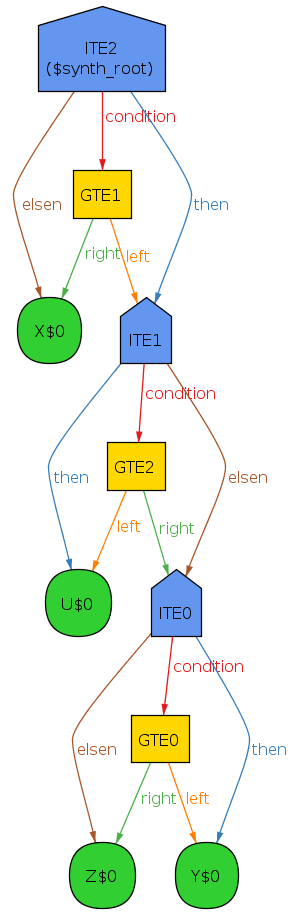
specification for max-4
one sig X, Y, Z, U extends Var {} pred spec[root: Node, eval: Node -> (Int + Bool)] { all v: Var | eval[root] >= eval[v] some v: Var | eval[root] = eval[v] }
generic synthesis predicate
pred synth[root: IntNode] { all env: Var -> one Int | some eval: Node -> one (Int+Bool) when env in eval && semantics[eval] | spec[root, eval] }
solving the synth predicate
run synth for 10 but 0..3 Int, exactly 3 ITE, exactly 3 GTE

generated program
higher-order analysis options
| name | type | default | description |
| Solver | MiniSat/SAT4J/... | SAT4J | SAT solver to use. Selected solver must support incremental solving if higher-order solving is used, i.e., must be one of: MiniSat, SAT4J, Glucose, CriptoMiniSat. |
| Use higher-order solver | yes/no | no | Enable/disable higher-order solver. |
| Create relations for atoms | yes/no | yes | Whether to create a Kodkod relation for each atom;
must be set to "yes" when higher-order solving is used. |
| Force incremental CEGIS induction | yes/no | yes | Whether to force incremental solving even when the induction increment formula is not first-order (by using a first-order approximation instead); "yes" typically results in better performance. |
| Maximum number of CEGIS iterations | int | 100 | Maximum number of iterations per each CEGIS loop. |
| Save CEGIS candidates as | Viz/Text/Nothing | Viz | Whether to save intermediate candidate solutions and how:
|
| Save CEGIS counterexamples as | Viz/Text/Nothing | Viz | Whether to save intermediate counterexamples and how (same as above). |
| Save CEGIS formulas | yes/no | yes | Whether to save intermediate formulas (saved as plain text). |
| Save CEGIS partial instances | yes/no | yes | Whether to save intermediate partial instances (saved as plain text). |
